これまでの1~4項にてバンドギャップや真性半導体の概念がある程度理解できたかと思う。今回は半導体内におけるキャリア密度について説明する。これを理解することで半導体の電気抵抗の算出ができるようになり、電気特性と半導体物性を紐づけて理解する助けになる。
・真性半導体のキャリア密度
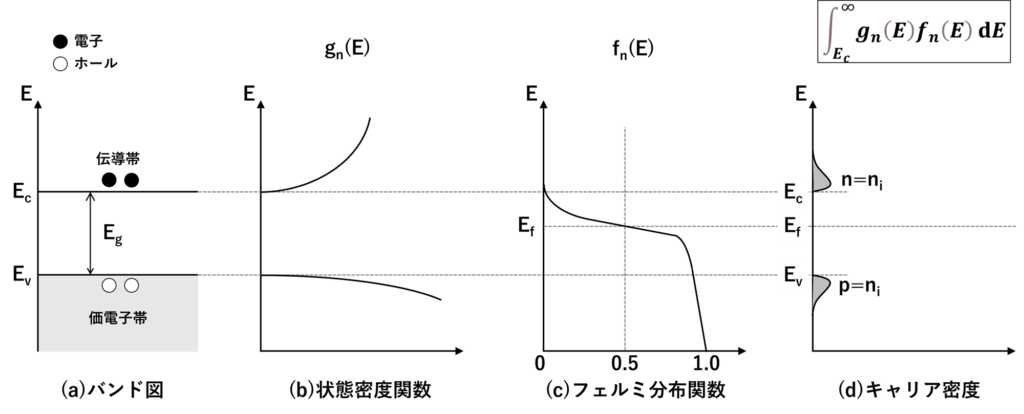
下図を見ながら真性半導体のキャリア密度を求めていきましょう。真正半導体でのキャリア(電流の担い手)は、価電子帯から励起された電子-ホール対により生成されるます。。この様子を表したのが(a)です。
図(b)は状態密度関数gn(E)と呼ばれており、与えられたエネルギー準位に対して、キャリアがどれくらいの密度で存在できるかを表したものです。あくまで”存在できるか”を表したものなので、この関数で表される量存在するというわけではありません。次に図(c)がフェルミ分布関数fn(E)となっています。これは電子の存在確率をを表したものです。これら状態密度関数gn(E)とフェルミ分布関数fn(E)をかけて積分することでキャリア密度が求まります。
・状態密度関数
図(b)~(d)について少し詳細に説明していきます。まずは図(b)の状態密度関数についてです。状態密度関数は単位面積あたりに電子が入ることができる数のことです。エネルギーが低いと少なく、高いと多くなります。状態密度関数gn(E)を数式で表すと下記となります。
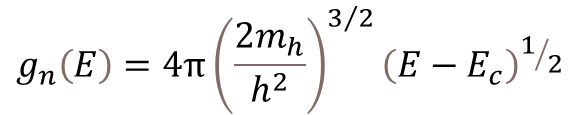
ここで、hはプランク定数、mhは電子有効質量です。有効質量以外は定数であり、gn(E)が(E-Ec)の1/2乗に比例することがわかります。ちなみに図(b)にて禁制帯(Eg) の範囲でgn(E)がのグラフが存在しませんが、これは禁制帯はキャリアが存在できないためです。
・フェルミ分布関数
図(c)フェルミ分布関数は電子の存在確率を示す関数となります。式で表すと下記のようになります。
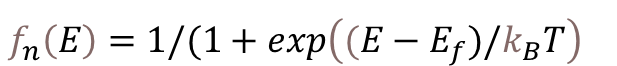
ここでkBはボルツマン定数で、Tは温度(ケルビン)である。この式はエネルギーEと温度Tの関数となっており、SiをTをパラメータとしてに分布関数を示したものが下図です。フェルミレベルEfを境に存在確率が0~1となる。※フェルミレベルは電子の存在確率が1/2のときのエネルギー準位。温度Tが大きいほど、同じエネルギーでも伝導帯の電子の存在確率が大きくなることがわかる。

・電子のキャリア密度
これまで説明した状態密度関数とフェルミ分布関数の積を示したのが図(d)電子のキャリア密度である。キャリア密度は単位面積当たりのキャリアの個数を表しており、Ec~Ev間(禁制帯)領域はキャリアが存在できないので電子の個数は0となっている。そして、価電子帯、伝導帯ではホール、電子それぞれのキャリア密度が示されているが、それぞれあるところでピークを迎えてそれ以降は0に近づいている。これはなぜか?キャリアが電子の時をみると、状態密度関数を見ると伝導体の上部に行くほど(=エネルギーが大きいほど)大きくなっている。状態密度関数は電子が入ることができる数、すなわち電子が座れる空席の数である。次にフェルミ分布関数を見るとエネルギーが大きいほど小さくなっている。フェルミ分布関数はキャリアの存在確率である。空席が多く、存在確率が大きいところがキャリアが最も存在するところになる。なので、エネルギーが大きくなるにつれて状態密度関数(空席の数)は大きくなるが、逆にフェルミ分布関数(キャリアの存在確率)はエネルギーが大きくなるにつれて小さくなっている。このため、両者が最もちょうどいいところでキャリアの数はピークを迎えてそれ以降は小さくなるというグラフの形になっている。ホールの場合も考え方は同じである。


コメント